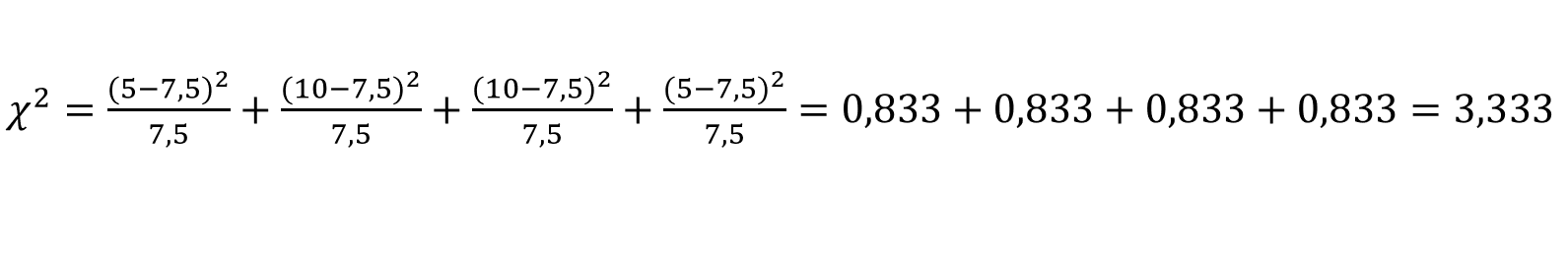5.2 Индуктивная статистика
5.2.1 Проверка статистических гипотез
Проверка статистических гипотез
Проверка статистических гипотез – это пятиступенчатая процедура, которая на основании данных выборки и при помощи теории вероятностей позволяет сделать вывод об обоснованности гипотезы.
Другими словами, этот способ проверить, действительны ли результаты, полученные на выборке, и для генеральной совокупности.
Люди «ошибочно уверенны» в своих знаниях и недооценивают вероятность того, что их убеждения могут оказаться ложными. Им свойственно искать искать такую дополнительную информацию, которая лишь подтверждает их собственные убеждения.
Макс Базерман
Пошаговый алгоритм:
1.Формулировка основной и альтернативной гипотезы
2.Выбор уровня значимости
3.Определение подходящего статистического критерия
4.Формулировка правила принятия решения
5.Принятие решения на основании данных выборки
Пол и частота пользования интернетом:
| Пол | |||
|
Пользование интернетом |
Мужской |
Женский |
Сумма по строке |
|
редко |
5 |
10 |
15 |
|
часто |
10 |
5 |
15 |
|
Сумма по столбцу |
15 |
15 |
n=30 |
Вопрос:
Можем ли мы на основании этой выборки утверждать, что во всем населении среди мужчин больше активных интернет пользователей, чем среди женщин?
Шаг 1: Формулировка основной и альтернативной гипотезы
Нулевая гипотеза (H0) – это утверждение статус-кво, что никакой разницы или никакого эффекта на самом деле нет.
Альтернативная гипотеза (H1) утверждает, что некоторая разница (или эффект) все таки должна быть.
H0: в отношении частоты пользования интернетом разницы между мужчинами и женщинами нет.
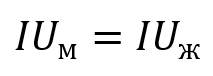
H1: мужчины и женщины пользуются интернетом с разной частотой.
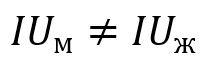
Шаг 2: Выбор уровня значимости
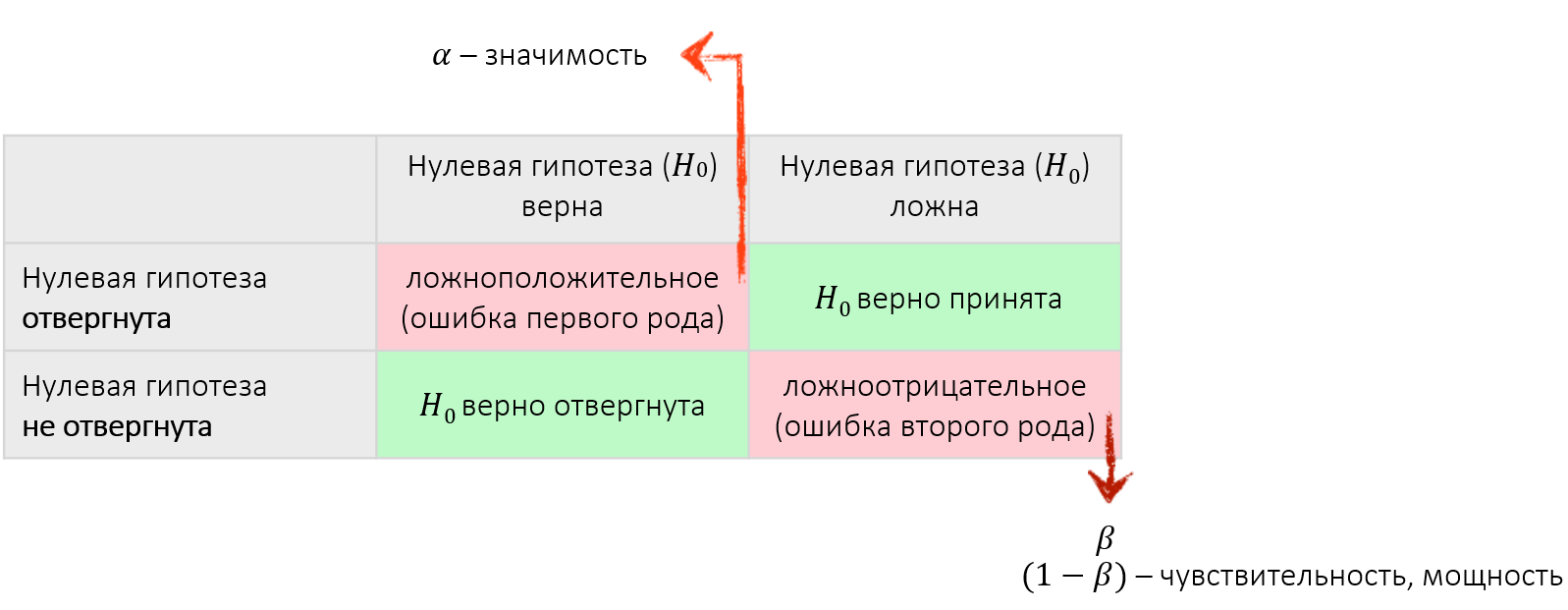
Значимость (α) – вероятность того, что верная нулевая гипотеза будет отвергнута.
β – вероятность того, что ложная нулевая гипотеза будет принята.
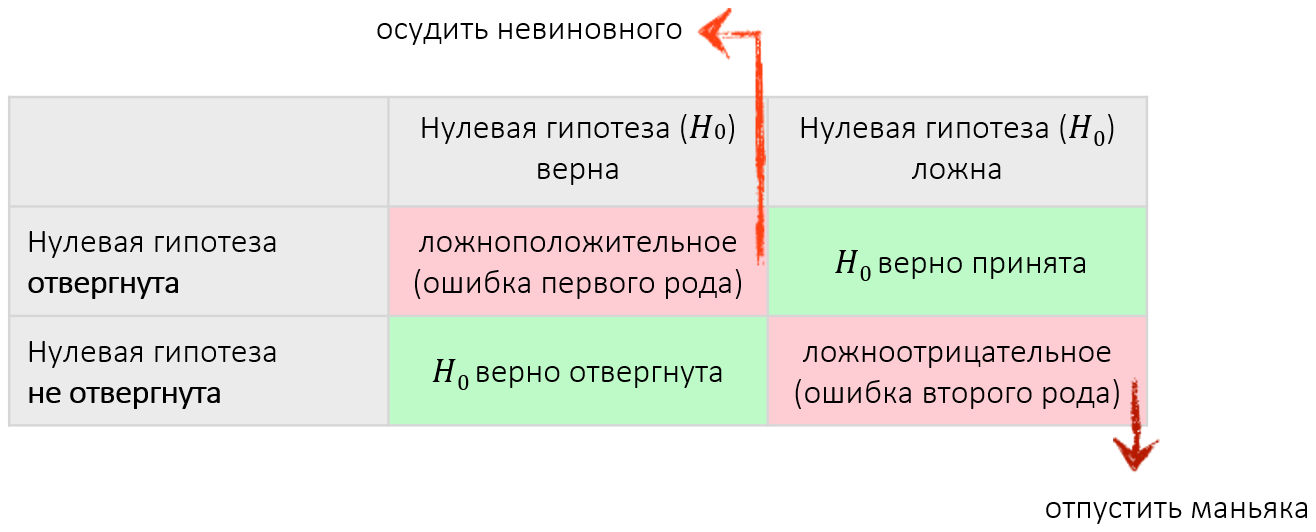
| Нулевая гипотеза (H0) верна | Нулевая гипотеза (H0) ложна | |
|
Нулевая гипотеза отвергнута |
ложноположительное (ошибка первого рода) |
H0 верно принята |
|
Нулевая гипотеза |
H0 верно отвергнута |
ложноотрицательное (ошибка второго рода) |
Аналогия: суд над маньяком
H0: заключенный не виновен
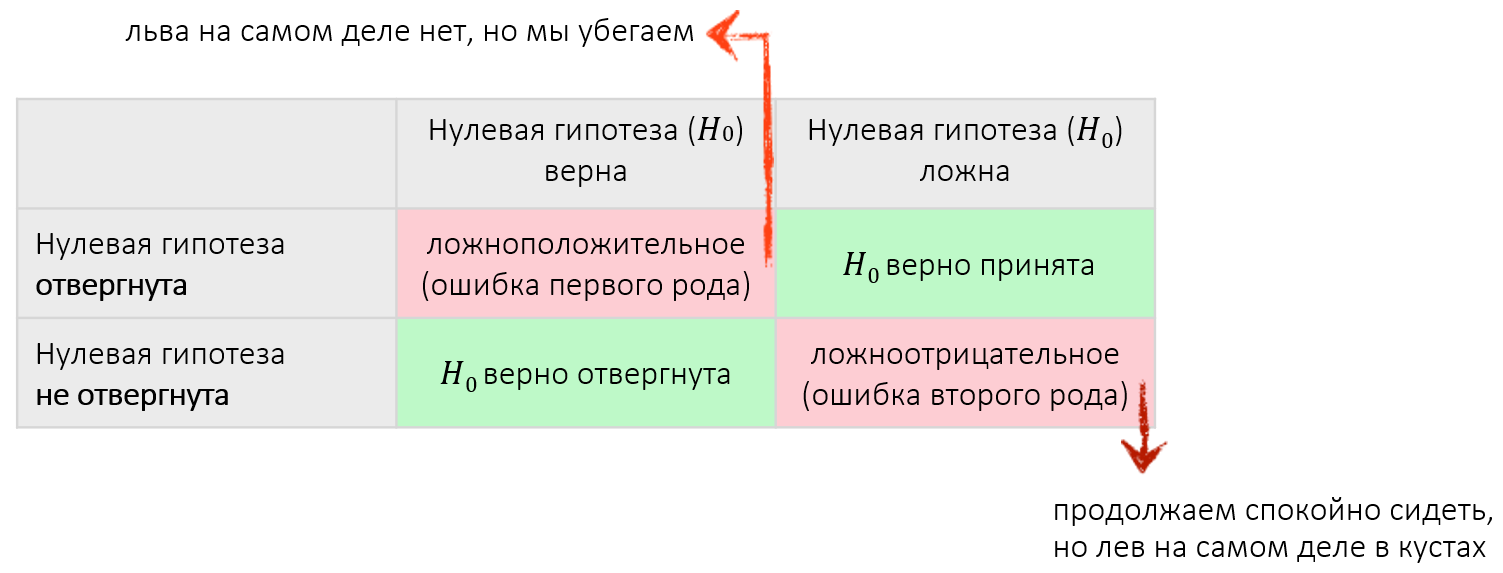
Аналогия: шорох в кустах – это лев?
H0: льва в кустах нет
Уровни значимости, принятые в маркетинговых исследованиях:
α – уровень значимости
0,01 (1%)
0,05 (5%)
(1-α) – уровень доверия (доверительная вероятность)
0,99 (99%)
0,95 (95%)
Шаг 3: Определение статистического критерия
Критерий χ2 (хи-квадрат) используется для проверки статистической значимости взаимосвязей между переменными, наблюдаемых в перекрестных таблицах.
H0: взаимосвязи между переменными нет
Тест χ2 проверяет равенство частотных распределений.
Какие распределения/частоты мы должны проверить?
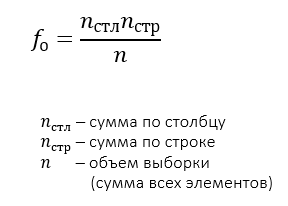
fо – ожидаемые частоты (расчётные значения), которые бы стояли в ячейках, в случае когда связи между переменными нет.
fн – реально наблюдаемые частоты, т.е. значения, которые стоят в составленной нами таблице
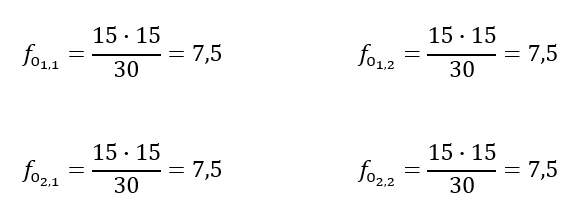
Расчёт χ2 следует производить только на основе абсолютных значений частот. Если исходные данные представлены в процентах, то их необходимо пересчитать а абсолютные частоты.
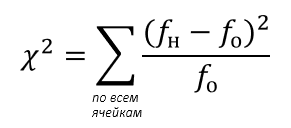
В нашем примере:
Шаг 4: Формулировка правила принятия решения
Kн – наблюдаемое (расчётное) значение статистического критерия.
Kкрит– критическое значение статистического критерия для заданного уровня значимости.
Если вероятность Kн меньше уровня значимости (α), то H0 надо отклонить.
или
Если Kн>Kкрит , то H0 надо отклонить.
Таблица критических значений χ2 для различных α
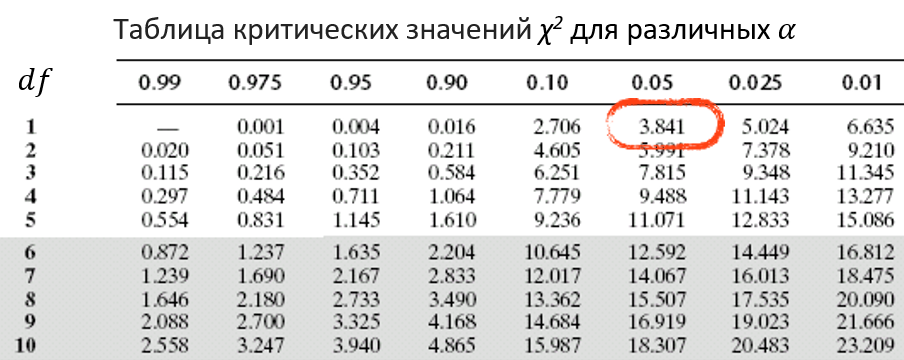
df=(r-1)(c-1)
df – количество степеней свободы
r – количество строк
c – количество столбцов
df=(2-1)(2-1)=1

H0 не может быть отклонена
Шаг 5: Принятие решения
Нашлись ли доказательства? Что из этого следует?
- H0 отсутствия различий не может быть отклонена
- Различия не являются статистически значимыми на уровне 0,05
- Полученные на выборке результаты не могут быть обобщены на генеральную совокупность
Пол и частота пользования интернетом
| Пол | |||
|
Пользование интернетом |
Мужской |
Женский |
Сумма по строке |
|
редко |
5 |
10 |
15 |
|
часто |
10 |
5 |
15 |
|
Сумма по столбцу |
15 |
15 |
n=30 |
Вопрос:
Можем ли мы на основании этой выборки утверждать, что во всем населении среди мужчин больше активных интернет пользователей, чем среди женщин?
Ответ:
Данная выборка не дает оснований для таких утверждений.
Если выборка была произведена должным образом, то мы можем с 95% доверительной вероятностью констатировать, что взаимосвязи между полом и частотой пользования интернетом нет. В противном случае – мы не знаем ответа.