5.5.1 Описательная статистика: Основные виды представления данных
5.1.3 Численное описание данных
Меры центральной тенденции
Среднее (арифметическое)
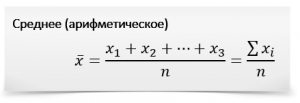
Среднее – это «центр тяжести», как точка баланса
Преимущества:
- удобная мера для получения представления о наборах данных, которые легко объединяются
- легко рассчитать: просто сложить и разделить
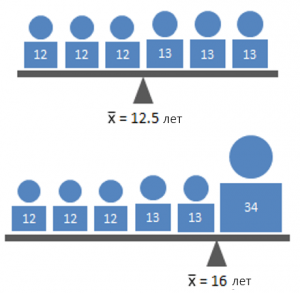
- Интуитивно – это число в середине, которое «тянут вверх» большие числа и «тянут вниз» маленькие числа.
Недостатки:
- среднее может быть легко отклонено нетипичными (выпадающими, экстремальными) значениями – плохо характеризует выборки с большой дисперсией.
- среднее значение 100, 200 и -300 = 0, что не интуитивно
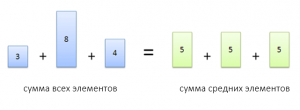
Медиана
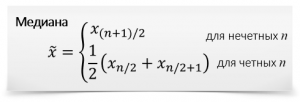
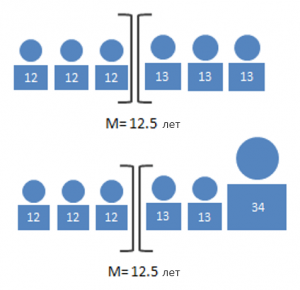
Медиана – это элемент в середине
Преимущества:
- нечувствительна к экстремальным значениям, часто описывает группу более точно
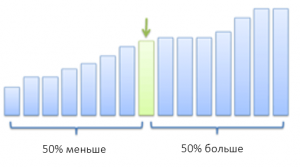
- разбивает данные на две группы с равным количеством элементов
Недостатки:
- сложнее вычислить: надо сначала отсортировать данные
- менее известна; если сказать «медиана», многие подумают, что Вы имеете ввиду «среднее»
Мода
Формула моды имеет следующий вид.
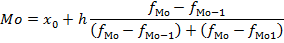
Где Мо – мода,
x0 – значение начала модального интервала,
h – размер модального интервала,
fМо – частота модального интервала,
fМо-1 – частота интервала, находящего перед модальным,
fМо1 – частота интервала, находящего после модального.
Мода – это самое частое наблюдение

Преимущества:
- хорошо подходит для ситуаций однозначного выбора типа «голосования» (что выбрать – то или это?), в особенности для номинальных шкал
- показывает выбор большинства респондентов (в то время как среднее может указывать на элемент, который никто не предпочитает).
- легка для понимания
Недостатки:
- требует больше усилий для вычисления (придется подсчитывать голоса за каждый элемент)
- «победитель получает все» – среднего не дано, нет компромиссного пути
Меры центральной тенденции:
как среднее и медиана описывают форму распределения
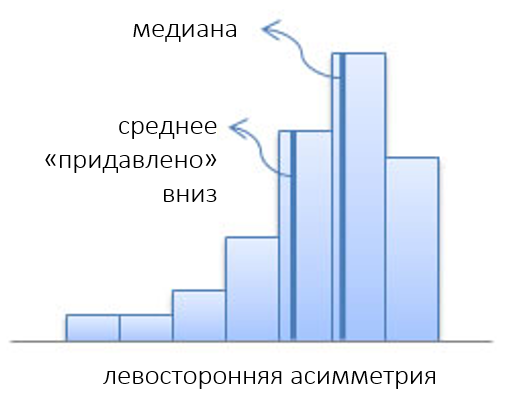
Левосторонняя асимметрия
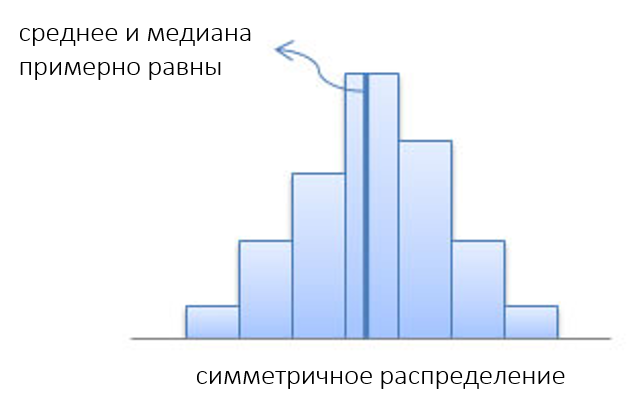
Симметричное распределение
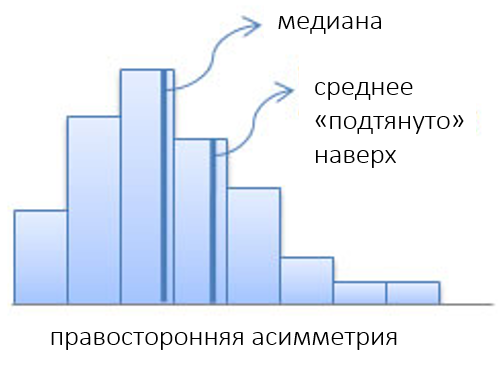
Правосторонняя асимметрия
Меры рассеяния
Дисперсия – среднее значение квадрата отклонения от среднего
Дисперсия генеральной совокупности:
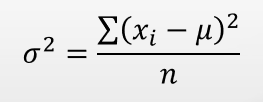
Дисперсия выборки:
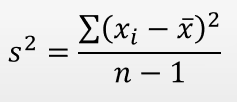
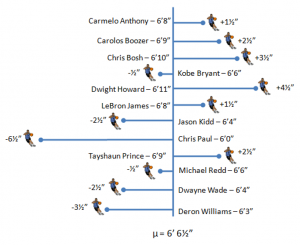
Рост членов олимпийской команды США по баскетболу (2008г)
Почему дисперсия?
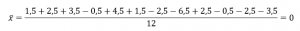
Среднее – это точка баланса. Поэтому среднее отклонение от среднего всегда равно нулю.
При вычислении дисперсии все отклонения возводятся в квадрат, чтобы положительные отклонения не компенсировали отрицательные отклонения.
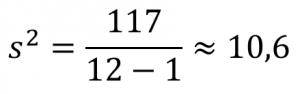
Меры рассеяния
Стандартное отклонение:
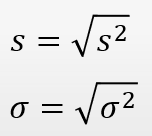
Стандартное (среднеквадратическое) отклонение сохраняет единицы измерения исходной величины

У какого набора данных стандартное отклонение больше?
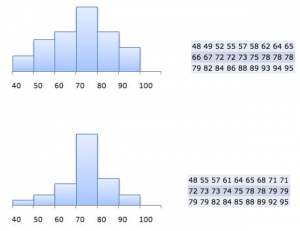
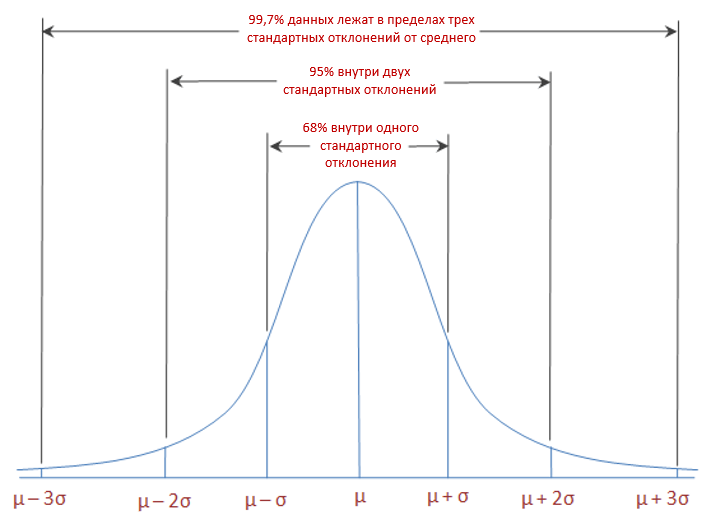
Взаимосвязь между стандартным отклонением и формой нормального распределения