5.5.1 Описательная статистика: Основные виды представления данных
5.1.2 Представление количественных данных
Таблицы
Исходные данные
|
2 |
2 | 2 | 4 | 5 | 3 | 3 | 3 | 3 |
|
2 |
1 |
2 |
3 |
5 |
3 |
4 |
3 |
1 |
|
2 |
3 |
5 |
3 |
2 |
1 |
3 |
2 |
|
|
количество детей |
частота |
относительная частота |
|
|
1 |
3 |
3/26≈ |
0,12 |
|
2 |
8 |
8/26≈ |
0,31 |
|
3 |
10 |
10/26≈ |
0,38 |
|
4 |
2 |
2/26≈ |
0,08 |
|
5 |
3 |
3/26≈ |
0,12 |
Дискретная переменная – это такая переменная, которая может принимать значения только из некоторого конечного списка возможных значений, например, 0, 1, 2, 3, …
Иногда категорий слишком много, так что нет смысла заводить для каждой из них новую строку. В таком случае следует объединить несколько категорий в группы (или «классы»).
Исходные данные
|
62 |
87 | 67 | 58 | 95 | 94 | 91 | 69 | 52 |
|
76 |
82 |
85 |
91 |
60 |
77 |
72 |
83 |
79 |
|
63 |
88 |
79 |
88 |
70 |
75 |
75 |
|
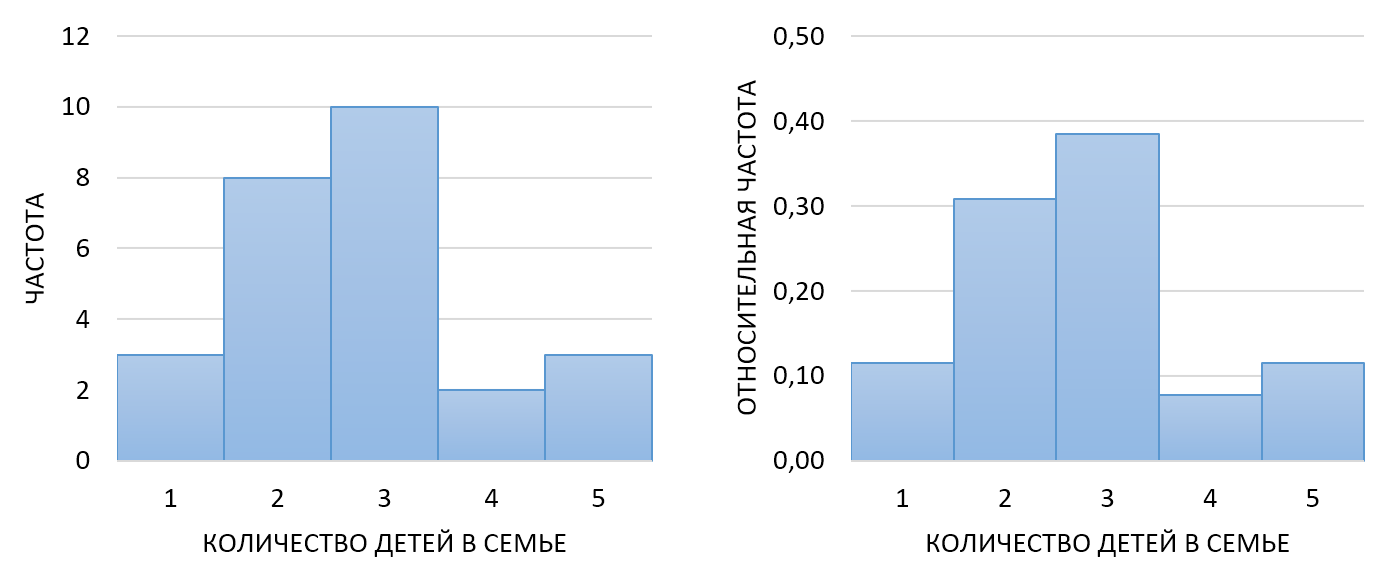
Гистограмма
Гистограмма
- Высота столбцов показывает абсолютные или относительные частоты категорий
- Столбцы одинаковой ширины и касаются друг друга
Пример 1
| количество детей |
частота |
относительная частота |
|
|
1 |
3 |
3/26≈ |
0,12 |
|
2 |
8 |
8/26≈ |
0,31 |
|
3 |
10 |
10/26≈ |
0,38 |
|
4 |
2 |
2/26≈ |
0,08 |
|
5 |
3 |
3/26≈ |
0,12 |
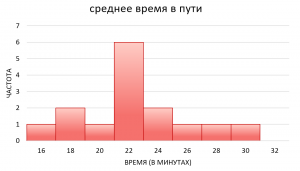
Пример 2
| среднее время в пути |
частота |
относительная частота |
|
|
16–17,9 |
1 |
1/15≈ |
0,07 |
|
18–19,9 |
2 |
2/15≈ |
0,13 |
|
20–21,9 |
1 |
1/15≈ |
0,07 |
|
22–23,9 |
6 |
6/15≈ |
0,40 |
|
24–25,9 |
2 |
2/15≈ |
0,13 |
|
26–27,9 |
1 |
1/15≈ |
0,07 |
|
28–29,9 |
1 |
1/15≈ |
0,07 |
|
30–31,9 |
1 |
1/15≈ |
0,07 |
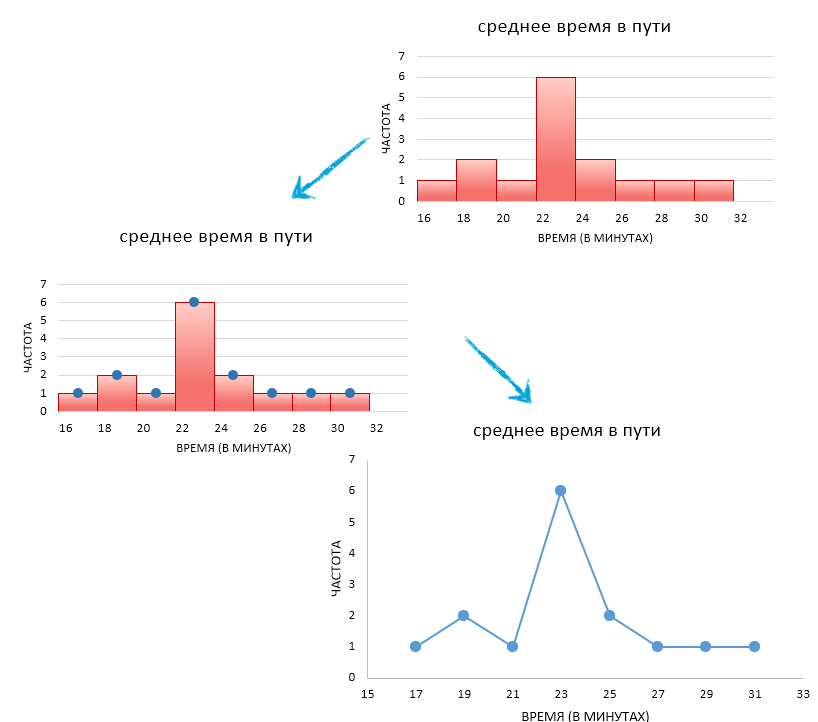
Полигон частот
Полигон частот - представляет собой ломанную линию, соединяющую центры вершин гистограммы, то есть точки, соответствующие серединным значениям интервалов группировки и частотам этих интервалов.
| среднее время в пути |
частота |
относительная частота |
|
|
16–17,9 |
1 |
1/15≈ |
0,07 |
|
18–19,9 |
2 |
2/15≈ |
0,13 |
|
20–21,9 |
1 |
1/15≈ |
0,07 |
|
22–23,9 |
6 |
6/15≈ |
0,40 |
|
24–25,9 |
2 |
2/15≈ |
0,13 |
|
26–27,9 |
1 |
1/15≈ |
0,07 |
|
28–29,9 |
1 |
1/15≈ |
0,07 |
|
30–31,9 |
1 |
1/15≈ |
0,07 |
Кумулятивная частота
Кумулятивная (накопленная) частота – сумма частот всех категорий, предшествующих определенной категории, включая ее.
| среднее время в пути | частота | кумулятивная (накопленная) частота |
| 16–17,9 | 1 | 1 |
| 18–19,9 | 2 | 3 |
| 20–21,9 | 1 | 4 |
| 22–23,9 | 6 | 10 |
| 24–25,9 | 2 | 12 |
| 26–27,9 | 1 | 13 |
| 28–29,9 | 1 | 14 |
| 30–31,9 | 1 | 15 |
| среднее время в пути | относительная частота | кумулятивная относительная частота | ||
| 16–17,9 | 1/15≈ | 0,07 | 1/15≈ | 0,07 |
| 18–19,9 | 2/15≈ | 0,13 | 2/15≈ | 0,20 |
| 20–21,9 | 1/15≈ | 0,07 | 1/15≈ | 0,27 |
| 22–23,9 | 6/15≈ | 0,40 | 6/15≈ | 0,67 |
| 24–25,9 | 2/15≈ | 0,13 | 2/15≈ | 0,80 |
| 26–27,9 | 1/15≈ | 0,07 | 1/15≈ | 0,87 |
| 28–29,9 | 1/15≈ | 0,07 | 1/15≈ | 0,94 |
| 30–31,9 | 1/15≈ | 0,07 | 1/15≈ | 1,00 |
Кумулята и огива
Кумулята – график, который показывает накопление частот при увеличении значения интересующей характеристики.
Сколько случаев имеют значение меньшее или равное значению категории?
Огива – показывает то же самое, только в «перевернутых» осях координат
| среднее время в пути | частота | кумулятивная (накопленная) частота |
| 16–17,9 | 1 | 1 |
| 18–19,9 | 2 | 3 |
| 20–21,9 | 1 | 4 |
| 22–23,9 | 6 | 10 |
| 24–25,9 | 2 | 12 |
| 26–27,9 | 1 | 13 |
| 28–29,9 | 1 | 14 |
| 30–31,9 | 1 | 15 |
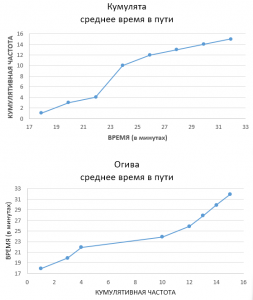
Парадокс: по-английски словом “ogive“ обозначается кумулята, огивы в англоязычном научном мире обычно не сторят.

