4.Выборка
4.4 Объем выборки
Определение объёма выборки
Объём выборки зависит не от размера изучаемой генеральной совокупности, а от качественных характеристик исследования.
- желаемая точность оценок,
- знание параметров генеральной совокупности
- количество переменных
- методы анализа
- важность принимаемого решения
- доля ответивших респондентов
- ресурсы

Типичные объемы выборок в маркетинговых исследованиях
| Тип исследования | Минимальный объем выборки | Типичный объем выборки |
|
Эксплоративные исследования (например, потенциал рынка) |
500 |
1,000 - 2,000 |
|
Каузальные исследования (например, ценообразование) |
200 |
300 - 500 |
|
Тесты продуктов |
200 |
300 - 500 |
|
Исследования на тестовых рынках |
200 |
300 - 500 |
|
ТВ/Радио/Печатная реклама |
150 |
200 - 300 |
|
Аудит тестовых рынков |
10 магазинов |
10 - 20 магазинов |
|
Фокус группы |
6 групп |
10 - 15 групп |
Определение объёма выборки на основании погрешности
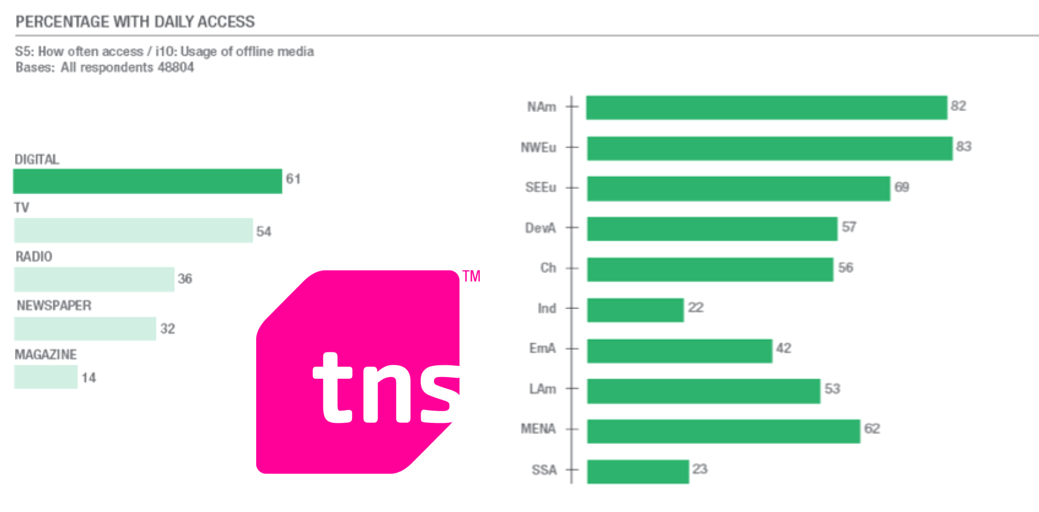
Определение объёма выборки на основании погрешности
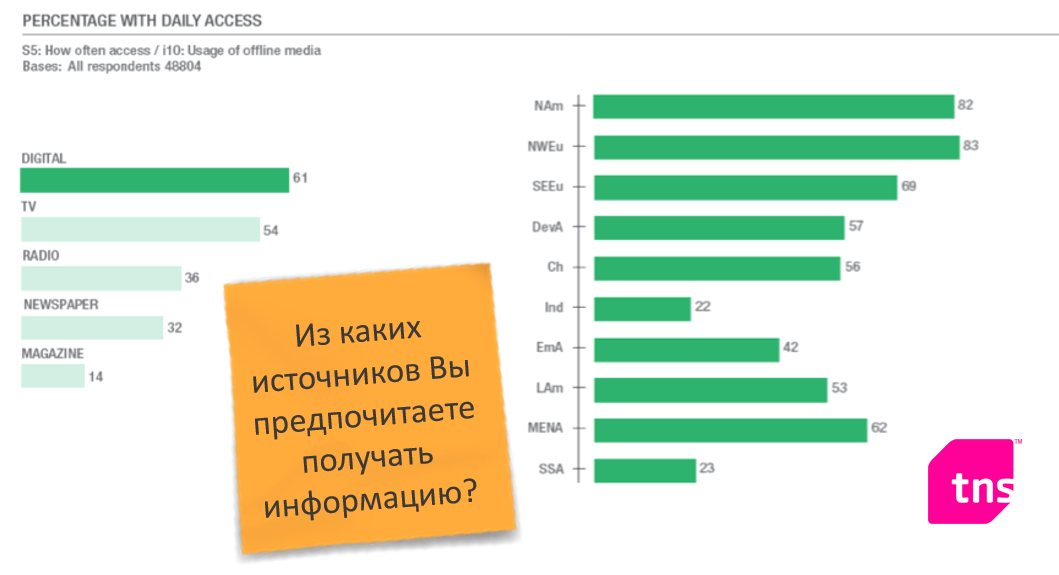
Определение объёма выборки на основании погрешности
Насколько точны полученные данные? Какова их погрешность?
Погрешность – это характеристика точности измерений в исследовании. Чем меньше погрешность, тем более точны оценки исследования.
Метод погрешности
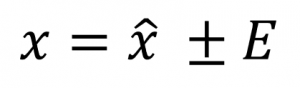
x = реальное значение параметра в генеральной совокупности
![]() = значение параметра в выборке
= значение параметра в выборке
E = погрешность
Средние значения
Используйте эту формулу для оценки точности средних значений генеральной совокупности, полученных на основе выборки.
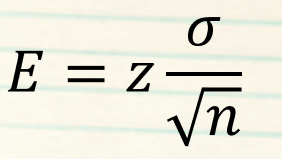
z = z-значение для заданного уровня доверительной вероятности
σ = стандартное отклонение параметра генеральной совокупности
n = размер выборки
Пропорции
Используйте эту формулу для оценки точности пропорций
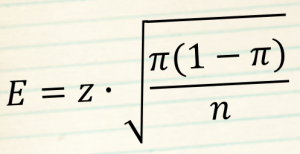
z = z-значение для заданного уровня доверительной вероятности
π = оценочное значение пропорции в генеральной совокупности
n = размер выборки
Где σ и π(1-π) - обычно не известны, а π(1-π) максимально при π = 0,5
z-значения
z = 1,96 - для доверительной вероятности 95%
z = 2,58 - для доверительной вероятности 99%
Максимальная погрешность для 95% доверительной вероятности
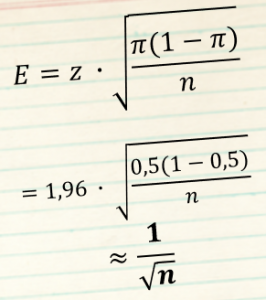
Метод погрешности
На сколько точны полученные данные? Какова их погрешность?
Погрешность = 1/√n
48 804 респондента в выборке
√(48 804)=220,916
1/221 = 0,0045
*100 = 0,45%
⇒ x = 61% ± 0,27% (0,27% = 0,45% от 61%)
⇒ 60,73% до 61,27%
приблизительные расчеты для доверительной вероятности 95%
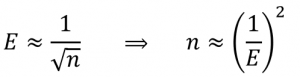
Каким должен быть объем выборки для погрешности ±1%?
Объем выборки = (1/погрешность)^2
n±1%= (1/0,01)^2 = (100)^2 = 10 000
n±2%= (1/0,02)^2 = 50^2 = 2 500
n±5%= (1/0,05)^2 = 20^2 = 400
n±10%= (1/0,1)^2 = 1062 = 100
приблизительные расчеты для доверительной вероятности 95%
Если объем выборки больше 10% генеральной совокупности, необходима корректировка
Объем выборки = (1/погрешность)^2
Объём выборки не зависит от размера генеральной совокупности
n±1%= (1/0,01)^2 = (100)^2 = 10 000
Что если генеральная совокупность состоит всего из 100 элементов? (напр., автозаводы)
приблизительные расчеты для доверительной вероятности 95%
Коррекция объема выборки
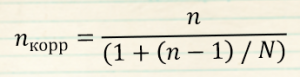
n_корр = скорректированный объем выборки
n = рассчетный объем выборки
N = размер генеральной совокупности
приблизительные расчеты для доверительной вероятности 95%
Если объем выборки больше 10% генеральной совокупности, необходима корректировка
Желаемая погрешность 1%
n±1%= (1/0,01)^2 = (100)^2 = 10 000
Что если генеральная совокупность состоит всего из 100 элементов? (например, автозаводы)
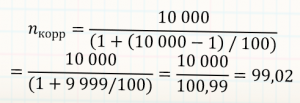
Желаемая погрешность 5%
n±5%= (1/0,05)^2 = (20)^2 = 400
Что если генеральная совокупность состоит всего из 100 элементов? (например, автозаводы)
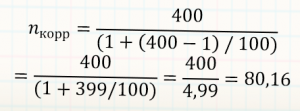
Желаемая погрешность 10%
n±10%= (1/0,1)^2 = (10)^2 = 100
Что если генеральная совокупность состоит всего из 100 элементов? (например, автозаводы)
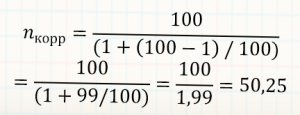
Доверительный интервал
доверительный интервал и доверительная вероятность
Доверительный интервал – это диапазон чисел, в котором находится истинное значение характеристики, измеренной на выборке.
Доверительная вероятность – это процент интервалов, которые будут содержать истинное значение, если мы повторим измерения на разных выборках много раз.
Предположим, нас интересует, сколько часов люди работают в день. Для этого мы взяли выборку из 30 респондентов и выяснили, что они работают в среднем 7,5 часов в день. Если мы говорим, что с 95%-ой доверительной вероятностью истинное среднее рабочее время находится в интервале от 7,2 до 7,8 часов, то это означает, что если мы повторим наши измерения на новых выборках и заложим погрешность в ±0,3 часа, то в 95% случаев наш интервал действительно будет содержать истинное значение.
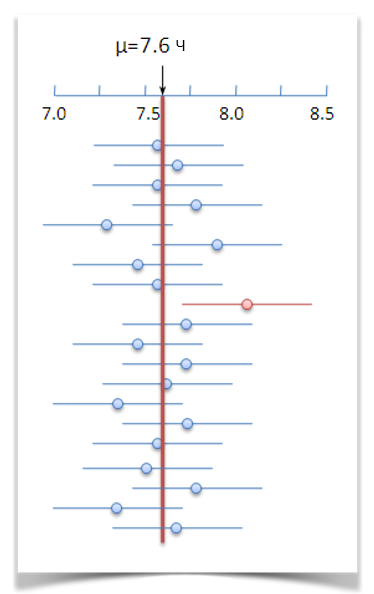
Чем выше выбранная нами доверительная вероятность, тем шире доверительный интервал и больше погрешность.
z-значения
z = 1,96
для 95% доверительной вероятности
z = 2,58
для 99% доверительной вероятности
Максимальная погрешность для 99% доверительной вероятности
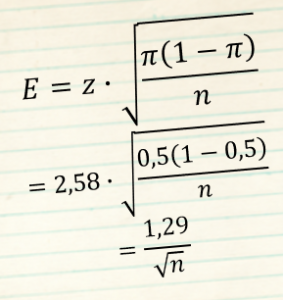
- для понижения погрешности нужна бóльшая выборка
- для повышения доверительной вероятности нужна бóльшая выборка
- чтобы уменьшить погрешность, надо увеличить объем выборки (корень из n)

